Parabola:
A parabola is a set of all points in a plane that are equidistant from a given fixed point (the Focus) and a given straight line (the Directrix).
Different cases of parabolas:
1) With the vertex at the origin, the parabola opens in the positive x direction and has the equation 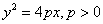 where vertex=(0,0) and focus is the point (p,0).
where vertex=(0,0) and focus is the point (p,0).
2) With the vertex at the origin, the parabola opens in the negative x direction and has the equation 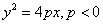 where vertex=(0,0) and focus is the point (p,0).
where vertex=(0,0) and focus is the point (p,0).
3) With the vertex at the origin, the parabola opens in the positive y direction and has the equation 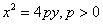 where vertex=(0,0) and focus is the point (0,p).
where vertex=(0,0) and focus is the point (0,p).
4) With the vertex at the origin, the parabola opens in the negative y direction and has the equation 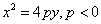 where vertex=(0,0) and focus is the point (0,p).
where vertex=(0,0) and focus is the point (0,p).
Definition of an ellipse:
An ellipse is a set of all points in a plane, whose distances from two fixed points (the foci) is a positive constant.
Different cases of ellipses:
1) The vertex is at the origin and the foci and the major axis are on the x-axis with the center at the origin and has the equation of the form 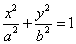 where the foci and the major axis are on the x-axis, the length of the major axis is 2a, the minor axis is on the y-axis, the length of minor axis equals to 2b and the center of the origin is at the origin (0,0).
where the foci and the major axis are on the x-axis, the length of the major axis is 2a, the minor axis is on the y-axis, the length of minor axis equals to 2b and the center of the origin is at the origin (0,0).
2) The vertex is at the origin and the foci and the major axis are on the y-axis with the center at the origin and has the equation of the form 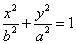 where the foci and the major axis are on the y-axis, the length of the major axis=2a, the minor axis is on the x-axis, length of the minor axis=2b and the center is at the origin (0,0).
where the foci and the major axis are on the y-axis, the length of the major axis=2a, the minor axis is on the x-axis, length of the minor axis=2b and the center is at the origin (0,0).
Definition of a hyperbola:
A hyperbola is a set of all points in a plane, the difference of whose distances from two fixed points (the foci) is a positive constant.
Different cases of hyperbolas:
1) The center is at the origin and the foci are on the x-axis and conjugate axis is the y-axis and has the equation of the form 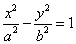 where the foci and the vertices are on the
where the foci and the vertices are on the
x-axis, the distance between the foci=2a, the conjugate axis is on the y-axis and the center is at the origin (0,0).
2) The center is at the origin and the foci are on the y-axis and conjugate axis is the x-axis and has the equation of the form 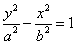 where the foci and the vertices are on the
where the foci and the vertices are on the
y-axis, the distance between the foci=2a, the conjugate axis is on the x-axis and the center is at the origin.
Asymptotic Equations:
The equations of the asymptotes to the hyperbola 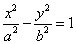 are as follows
are as follows 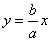 and
and 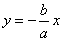 .
.



