Definition of a matrix:
Any 2-dimensional array of real or complex numbers.

Square matrix:
A matrix of type .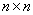

Diagonal:
The entries of a square matrix in the i-th line and i-th column (same index i), for some i.

Identity matrix:
A square matrix with 1’s on the diagonal and 0’s off the diagonal.

Zero matrix:
Any matrix (of any type), with only zero entries.

Definition of a 2-dimensional matrix:

We define of a 2-dimensional matrix as: .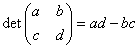

Definition of the rank of a matrix:
The rank of a matrix A is the greatest n such that A has a square sub-matrix of type nxn with determinant not equal to zero.

Definition of an invertible matrix:
We say a square matrix A is invertible if there exits a (square) matrix B such that AB=BA=identity matrix.

Cramer’s Rule:
If A is a square matrix, then the equation AV=w has a unique solution if and only if 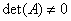and the solution is.

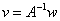Matrices are important tools in solving linear systems. Their properties and operations allow solutions to be arrived at in fewer steps than other traditional approaches to algebra problems. Performing computations with matrices is shown in this tutorial through the examples.

Determinants are used introduced so the idea of Cramer’s rule can be formulated. Cramer’s rule is a famous rule that uses determinants to finding solutions to a system of equations. Reducing matrices involving the addition or multiplication of rows and columns in a matrix

Specific Tutorial Features:

• The operations of matrices are shown in some of the examples.
• Performing computation with matrices is presented in the examples.
• Step by step explanation of the rank of a matrix with respect to a determinant is shown in a couple of examples.

Series Features:

• Concept map showing inter-connections of new concepts in this tutorial and those previously introduced.
• Definition slides introduce terms as they are needed.
• Visual representation of concepts
• Animated examples—worked out step by step
• A concise summary is given at the conclusion of the tutorial.